ChatGPT o1が東大数学で合格最低点を突破！生成AIの可能性と限界を探る

はじめに

この記事では，生成AIの最新モデル，ChatGPT o1に，東大数学の入試問題を解かせることで，数学教育への活用可能性とその限界を探ることを目的としています．大学院時代にAI関連研究で修士号を取得後，ソフトウェアエンジニアとしてキャリアを積んでいる，東大理系数学116/120点のSaki(@Saki_reset)が本記事の執筆・解説を行います．

ChatGPT o1とは？

近年、生成AIの進化は目覚ましく、その中でも昨日2024年9月14日に発表された，最新モデルであるChatGPT o1は特に注目を集めています。このモデルは、従来の言語モデルを大幅に超える論理的思考能力と計算力を備えており、複雑な問題解決にも対応できると言われています。

ChatGPT o1の凄さは、その高度なアルゴリズムと大量のデータ学習により、人間に近いレベルの推論や分析が可能になっている点です。では、このモデルは大学受験レベルの数学問題、特に東大理系数学にどこまで対応できるのでしょうか？その限界を探っていきます．

生成AI一般が大学受験数学に弱い理由

ChatGPT 4のような，o1以前の生成AIは，数学や物理などの課題には弱いとされてきました．特に，大学受験数学の答案作成という用途においては，あまり使い物になりませんでした．

その理由は主に以下の3点です。

1. 論理的思考が出来ないこと

生成AIは、大量のデータからパターンを学習(統計的機械学習)し、それを基に新しいテキストを生成します。しかし、数学の問題を解く際には、条件を正確に理解し、論理的な推論を積み重ねて解答に至る必要があります。従来の生成AIは、文章の統計的な関連性を学習しているため、深い論理的推論を必要とする問題に対しては適切に対応できません。

2. 計算ミスを犯すこと

生成AIは、数値計算を専門として設計されていないため、計算ミスを犯すことがよくあります。

• 数値の扱いの問題: 生成AIは数値をテキストデータとして扱います。そのため、実際の計算を行うのではなく、数字のパターンを基に次の数字を予測します。この方法では正確な計算結果を得ることが難しいです。
• 桁数や複雑な計算への弱さ: 複雑な計算や大きな数値を扱う際に、計算過程で誤りが生じやすくなります。これは、モデルが計算アルゴリズムを理解しているわけではないためです。

3. 高校生の持つ知識に沿った答案の作成が出来ないこと

生成AIは、インターネット上の膨大なデータを学習しているため、大学レベルや専門的な知識も含まれています。

• 範囲外の知識の使用: 高校生が学習していない高度な数学的概念や特殊な解法を用いて解答を生成してしまうことがあります。受験では高校範囲の知識が評価対象の中心となるため、これは減点の原因となり得ます。
• 解答形式の不適切さ: 受験では解答の書き方や論述の形式も重要です。生成AIは、その場に適した解答形式を理解していないため、採点基準に沿わない答案を作成する可能性があります。
• 専門用語や高度な記法の誤用: 高校生が使わない専門用語や高度な数式表現を用いることで、解答が不適切になる場合があります。

大学受験数学への弱点の対処方法

1．最新モデルo1を用いる

従来のモデルは文章生成には優れていましたが、複雑な論理的思考を必要とする数学問題には対応が困難でした。しかし、ChatGPT o-1では高度な論理思考が可能となり、この問題は大幅に解決されています。

2. 計算ミスへの対処 – プロンプトエンジニアリング

計算ミスは生成AIの大きな課題の一つです。しかし、通常のコンピューターでは，数値計算は最も得意とする分野です．従って，最新の生成AIと，通常のコンピューターをうまく組み合わせることで，計算ミスは回避できます．具体的には，プロンプトに指示を与えることで、この問題を軽減できます。

例えば、「ただし、数式の計算や、図を描画する際には、必ずPythonのプログラミングを使用して、計算ミスが起こらないように注意してください。」といった指示を加えることで、計算の正確性が飛躍的に向上します。

3. 高校範囲での答案作成 – プロンプトエンジニアリング

生成AIは時に大学レベルの知識や独自の解法を用いてしまうことがあります。これを防ぐためには、プロンプトで「高校生が学習する範囲の知識のみを使用すること」と明示することが重要です。例えば，以下のようなプロンプトが考えられます．

この問題は、日本の高校生に対して出題される問題です。したがって、解答には高校で習う程度の数学の知識のみを用いて解答してください。積分や関数の解答の値は、log、In、exp、sqrt、sin、cosを用いて、解析的な形で必ず表現してください．

完成したプロンプト

以上の対策を踏まえ、以下のようなプロンプトを用意しました。

あなたは、国際数学オリンピックの金メダリストです。
以下の数学の問題の解答を作成してください。ただし、解答作成の際は、以下の点に留意してください。

1. この問題は、日本の高校生に対して出題される問題です。したがって、解答には高校で習う程度の数学の知識のみを用いて解答してください。積分や関数の値は、log、In、exp、sqrt、sin、cosを用いて、解析的な形で必ず表現し、数値積分は用いないでください。
2. この問題の解答には、基本的にプログラミングを使用せず、数学的な論理展開・式変形に基づく議論に基づいて、解答を作成してください。ただし、数式の計算や、図を描画する際には、必ずPythonのプログラミングを使用して、計算ミスが起こらないように注意してください。
3. 図を描画する問題は、matplotlibを用いて、解答の図も作成してください。
4. 「全て求めよ。」という指示の問題に対しては、考え得る答えの組以外に、ほかの組み合わせが存在しないということも、数学的な議論に基づいて、証明してください。
5. 「であることを示せ。」という指示の問題は、証明問題です。したがって、いくつかの具体的な数値で成り立つことを証明するだけでなく、数学的な議論に基づいて、題意を満たす全ての場合について、命題が成立することを証明してください。

以上の指示に基づいて、以下の問題の解答を作成してください:

# 問題

ここに問題を書く．

# 解答

プロンプトの意図

1. は，高校範囲の数値表現で解答するというレギュレーションです．対数の値(たとえば，log2)をそのまま数値計算して表現してしまったり，逆三角関数などを用いた解答の表現の出力も見られたため，具体的に使える関数を提示しています．また，積分の問題において，解析的に計算出来るのにも関わらず，数値積分を用いた方法を提示してきたため，数値積分はするなという指示を与えています．
2. は，特に整数問題の証明などについて，プログラミングを駆使して，最初の100個の組み合わせについて実験をし，全ての場合について成立しているので主張は成立する．という出力をすることが多く見られました．数学の答案ですので，当然最初の数で実験しただけでは証明は成立せず，論理的に全ての場合について成り立つことを証明しなければいけません．そこで，基本的にはプログラミングを使用しない，という指示を与えています．ただし，計算ミスを回避するために，計算をする場合にだけ，使用を許可しています．
3. 軌跡と領域など，図を描画する必要のある問題への対応です．
4. 2とほぼ同じ理由です．
5. 2とほぼ同じ理由です．

東大理系数学2024を解かせる

さて，ここから実際に上記のプロンプトを与えて，東大理系数学2024をChatGPT o1に解かせてみましょう．

実際にChatGPT o1に東大理系数学2024年の問題を解かせたところ、解答時間544秒，120点満点中55点という結果になりました。概ね，東京大学理科二類の合格者ボーダーが，55点くらいですので、ChatGPT o1は，東大理系合格者の数学力のボーダーに達しており，その実力は真に驚くべきものです。

また，東大受験生は，この問題を150分，つまり9000秒掛けて解きますが，ChatGPT o1はその15倍の速さで解答を導けています．

さて，ここから実際に各問題の出力結果を見て，その恐ろしさと，限界について考察していきましょう．

第1問

問題

座標空間内の点 A(0, −1, 1) をとる。xy 平面上の点 P が次の条件 (i), (ii), (iii) をすべて満たすとする。

(i) P は原点 O と異なる。

(ii) ∠AOP ≧ \(\frac{2\pi}{3}\)

(iii) ∠OAP ≦ \(\frac{π}{6}​\)

このとき，P がとりうる範囲を xy 平面上に図示せよ。

ChatGPT o1の解答

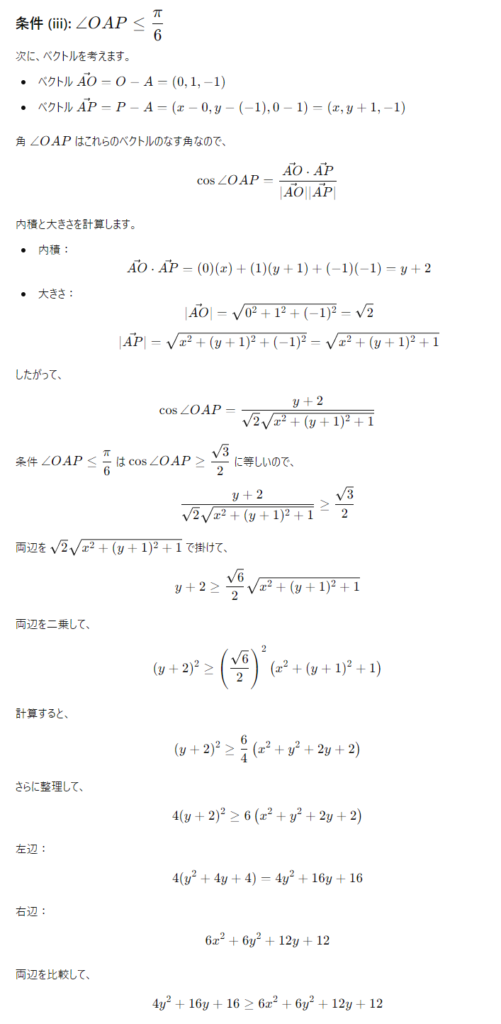
思考時間: 98秒 得点：17/20

立式から解答まで非常に的確です、ほぼ完璧な解答を提供しました。

原点を入れてしまっているので，減点とします．

第2問

問題

次の関数\(f(x)\)を考える。

\(f(x) = \int_0^1 \frac{|t – x|}{1 + t^2} \, dt \quad (0 \leq x \leq 1)\)

\((1) 0 < \alpha < \frac{\pi}{4} を満たす実数 \alpha で、f'( \tan \alpha ) = 0 となるものを求めよ。\) \((2) (1) で求めた \alpha に対し、\tan \alpha の値を求めよ。\) \((3) 関数 f(x) の区間 0 \leq x \leq 1 における最大値と最小値を求めよ。必要ならば、0.69 < \log 2 < 0.7 であることを用いてよい。\)

ChatGPT o1の解答

思考時間: 125秒 得点：12/20

(1)で計算をする際に，微積分学の基本定理に関する部分で若干の誤解が見られました．また，(3)でf(0)とf(1)の値の比較を明示的に行っていないなどの問題はありますが，全体的にはほぼ満点の解答でした。

第3問

問題

ChatGPT o1の解答

思考時間: 85秒　得点: 10/20

(2)の記述がやや不鮮明です．また，(3)については，状態数の分類と，それに基づく漸化式の立式までは正確でしたが、その後の計算に誤りがあり、正しい答えに至りませんでした。

第4問

問題

ChatGPT o1の解答

思考時間: 91秒 得点：9/20

(1)は少し複雑な計算でしたが，正確に正答が出来ています．さすがの計算力です．

(2)については，途中の式整理までは完璧に出来ていましたが，定数分離という受験数学の典型的な解法を知らなかったため、解答できませんでした。

第5問

問題

ChatGPT o1による解答

思考時間: 91秒 得点：0/20

中心軸からの最近傍点と最遠点を考えるという，回転体の問題における重要な視点が欠けていました．これも受験数学の典型的な考え方です．

第6問

問題

ChatGPT o1による解答

思考実験: 64秒 得点：7/20

(1)は正解していましたが，(2)は論理の展開に失敗し、解答を導き出すことができませんでした。

大学入試数学における生成AI活用の現状の能力

計算力

計算力は非常に高く、ほとんど計算ミスがありませんでした。プロンプトでの指示により、AIの弱点を克服できたと言えます。

答案構成力

解答の構成も素晴らしく、高校数学程度の知識を用いながら，数値計算や数値積分を回避し、ほとんどの場合について解析的な答えをきちんと提供できていました。

受験特有の定石

ここが最大の課題でした。漸化式の解き方、定数分離、ドーナツ型の断面図の積分など、受験数学で頻出する典型的な解法や知識が不足しているようです。これは、Few-Shot Learningというプロンプトエンジニアリングの手法を用いる，つまり具体例の問題とその解答を与えることで，改善の余地があります。

結論

ChatGPT o1は東大理系数学で合格最低点を超える実力を示しました。これは、ほとんど多くの高校生がこのAIよりも数学ができないことを意味します。

特に注目すべきは、このモデルがまだプレビュー版であり、これよりも精度が高い本格的なo1モデルが存在することです。これまで統計的機械学習に基づく生成AIが不得意とされてきた数学の論理的思考においても、AIが人間に迫る勢いで進化しています。

今後、ただ試験問題を解けるだけの人材の価値は急速に低下するでしょう。これから求められるのは、問題を発見できる人間や、どの問題を解くべきかを適切に判断できる人材です。

受験生の皆さんも、AIとの共存を視野に入れ、自らの価値を高める学習に取り組んでいくことが重要だと思います．