本記事の目的
この記事の目的は、数学の筆記試験で、得点のブレを最小限に抑えながら、得点の期待値を最大化する理論体系「110s -Double One Zeros-」について説明することです。数学の得点は、単に「その問題の解法を知っているか」という要因だけでなく、「どの解法を選択するか」という「戦術」の選び方や、「どの問題を選択するか」という「戦略」の選び方に応じて、大きく変動します。本理論体系110sでは、こうした「戦術」や「戦略」にスポットを当て、数学筆記試験本番で、どのような立ち回りをするのが最適か、考察する枠組みを提供します。
本記事で紹介する理論体系110s – Double One Zeros – の汎用性は高く、「高難易度の算数・数学の筆記試験全般」に適用できる基本的な枠組みであると考えています。なぜなら、筆者は、東大理系数学116点、東大模試数学偏差値90、アクチュアリー試験、統計検定1級、東大大学院入試など、種々の高難易度の数学の試験を高成績で突破しており、こうした自身の具体的な経験により得られた暗黙知を、抽象的な理論体系として編纂したものだからです。
対象読者
本理論体系110s – Double One Zeros – は、高難易度かつ制限時間の厳しい数学の試験に対する枠組みであり、以下のような読者を対象としています。
- 東大・京大・医学部受験生
- アクチュアリー試験・統計検定1級受験生
- 数理科学系大学院入試受験生
- 難関中学受験生とその保護者
110s – Double One Zeros – に込めた意味
本理論体系110s – Double One Zeros – には2つの意味を込めています。
- 東大理系数学高得点(110↑&6完)を目指す
東大理系数学の入試は、日本を代表する高難易度数学試験です。本理論体系は、その東大理系数学で、120点満点中110点台を獲得した筆者が、これから高難易度数学試験を受験する人たちに対して、同じように高得点を目指してほしいという願いを込めています。また、110は2進法で「6」であり、全6問構成の東大理系数学で6問完答するという意味も込めています。 - 二つの10sに贈る理論体系
10sには、「10代の若者、ティーンエイジャー」という意味があります。そして、10代の若者が再び「10s」を迎えるのは、その百年後、「110s」になった時です。本理論体系は、高難易度数学試験に初めて直面する10代から、110代になるまでの100年間に渡って、変わらずに意味を持ち続ける枠組みでありたい、そんな想いを込めています。
数学筆記試験の理論体系110sの全体像
最初に、数学筆記試験における得点最適化の理論体系110sの概観図を示します。これは、数学の筆記試験本番における、以下のような基本的な立ち回り方を、抽象的な枠組みに落とし込んだものです。

- 問題選択: 試験開始と同時に、まず全ての問題に目を通し、どの問題を解くべきか「問題選択」を行う
- 優先順位付け: 次に、選択した問題を、どの順番で解くか「優先順位付け」を行う
- 解法選択: 優先順位付けに基づいて、問題を解いていく。その際に、どの解法を用いるのが、最も速く正確に解答できるかを考える「解法選択」を行う
- 解法選択が見えなければ、「問題選択」フェーズに戻り、別の問題を選択する。
- 論理展開 & 計算実行: 解法選択が見えれば、それを「実行」するフェーズに移行する。適切な「論理展開」になっていることを意識しながら、「計算実行」を進める。
- 「計算実行」の際は、最も効率的に解ける「計算法選択」を行う。
- 「計算実行」のつど、適切なタイミングで「検算」を行う。
- 解答: 計算を済ませ、無事に正答を導く。検算が容易に出来るものについては、答えが合っているか確認する。
以上が、理論体系110sの全体像となります。次に、各ステップについて、もう少し詳細に論じます。
筆記試験の「戦略」
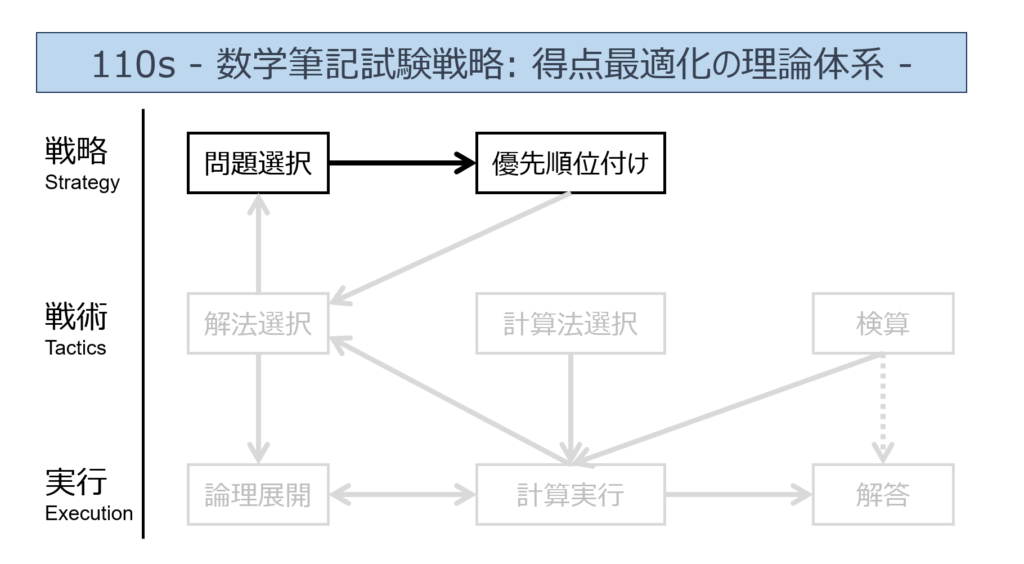
問題選択
数学の筆記試験で得点を取るために極めて重要な要素、それが、「問題選択」です。
試験が終わった後で、「実はあの問題が簡単だったが、時間が無くて手を付けられなかった」という後悔をしたことがある人も多いでしょう。問題選択の誤りは、容易に数十点単位の得点の損失を招きます。それ故に、自分が解ける難易度の問題を適切に見極めて、試験会場で問題選択が出来るようになることが重要です。
このように、問題選択及び、それを適切に行う能力-選球眼-は、極めて重要ですが、その鍛え方や、実際の試験において、どのような枠組みに基づいて問題選択を行ったのか、具体例を解説している情報はあまりありません。メタスキリングでは、こうした問題選択の方法論について、確かな経験と豊富な具体例に基づいて、体系的に論じます。
問題選択について論じた記事
優先順位付け
- 解くべき問題を選んだ後は、解く順序を決める必要があります。
- 問題の難易度や得点配分、自分の得意分野を考慮して、最も効率的な順序で解き進めます。
- 実質的には、「問題選択」と並行して順位付けが行われていることが多いです。
「戦術」の選択

こうして、問題選択及び、優先順位付けにより、解くべき問題とその順序が決まったら、各問題を「戦術」により攻略していくフェーズに移ります。「戦術」には、「解法選択」「計算法選択」「検算」の三要素がありますが、このうち最も重要で、得点に影響を与える要素は、「解法選択」です。
解法選択
解法選択には、「解法探索」と「解法選択」の2つのフェーズがあります。
- 解法探索: 問題文の題意を正確に把握し、そこから解答に至るまでの方針を、大雑把にいくつか積み上げるフェーズ
- 解法選択: 「探索」フェーズで大雑把に積み上げた方針の中から、高速かつ正確に、正答に辿り着ける解法を選ぶフェーズ
分かりやすさのために、簡単な具体例を挙げてみましょう。
具体例: 図形の面積の最大最小問題
- 解法探索: 辺の長さか角度をパラメータに設定して、そのパラメータの関数として面積を求めれば、あとはパラメータの制約条件の下での、関数の最大最小問題に帰着しそうだ、という方針を立てる。
- 解法選択: 辺の長さと角度のどちらをパラメータに設定するのが適切かを選ぶ。
解法選択を見誤ると、正答に辿り着けはするものの、計算の泥沼にはまり、膨大な時間を浪費してしまったり、計算を間違えてしまいます。それ故に、適切な解法を選ぶことが重要です。
多くの参考書では、ひとつの問題に対して、ひとつの解法のみを解答として載せており、その解法を選択するに至った思考過程・その解法を選択する必然性について、言及していることは少ないです。 メタスキリングでは、こうした事情を踏まえ、解法選択の方法論について、体系的に論じます。
「戦術」の「実行」
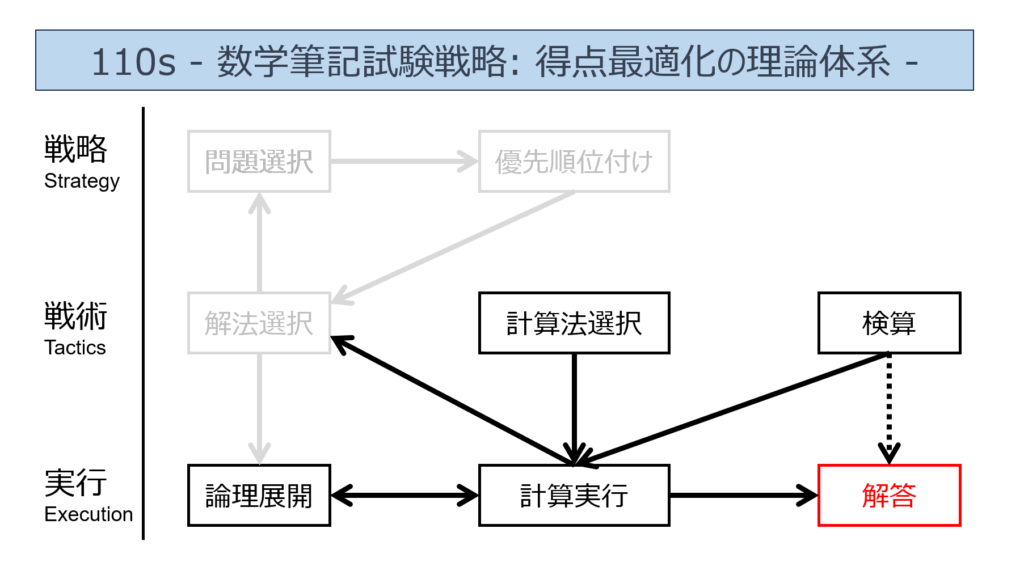
「実行」フェーズでは、「戦術」により確定した解法を、具体的に実行します。うまく計算が運べば、解答を導けます。一方で、計算が重たすぎたりした場合は、「解法選択」が間違っている可能性があるので、再び「戦術」フェーズに戻り、「解法選択」を考えることになります。
論理展開
選択した解法を、論理展開に誤りが無いように、丁寧に組み立ててます。ここを誤ると、正答にはたどり着けません。文字式を整理する際に、意外と盲点になることが多いのが、この「論理展開」という要素です。例えば、文字で割り算する際に、ゼロ除算を考慮しなかったり、不等号の場合分けが必要であったりすることは、意外と忘れがちです。
論理展開の漏れは、他人から添削を受けて、答案から減点されることで、初めて気づくというケースが多く、多くの受験生が苦手としている部分なのではないかと思います。メタスキリングでは、こうした盲点にメスを入れ、犯してしまいがちな論理展開の誤りについて論じます。
計算実行
論理展開と並行して、具体的な計算式が実行されます。計算を行う際には、複数の計算法から、最も速く正確に計算出来る方法を、毎回選択できるようになっていることが理想です。また、ミスが多発しやすい式変形については、計算が合っているかを、逐次検算することが望ましいです。
ここで計算実行がうまくいかなければ、解法選択に誤りがあったと判断して、「戦術」フェーズに戻り、再び解法を練ることになります。
解答
計算の実行が無事に終わると、解答が得られます。解答の妥当性を確認する方法として、検算が使える場合は、必ず検算をするべきです。
例えば、一般項nを求めているのであれば、n=1, 2のときに成立するかを確かめることはマストですし、極限の場合は大雑把な近似によって求めた結果と一致するかを確認する、という検算方法を適用することもできます。
「どういう問題であれば、一瞬で検算により答えをチェックできるか」を把握しておくことは、安定した得点を獲得するために、大事なテクニックとなります。こちらの「検算」についても、今後メタスキリングで論じていくテーマにする予定です。
以上が、本理論体系110s – Double One Zeros – の概要となります。
各論についての具体的な能力の鍛え方や、具体的な入試問題のセットについて、110sを適用して、どのように得点を取っていくのか、という個別事例については、今後の記事にて執筆していく予定です。
東大理系数学2024について、110sに基づいて解説した記事
最後に: 110s の活用法
本記事で紹介した数学筆記試験得点最適化の理論体系110sは、高難易度試験で高得点を取る人が、試験本番でどのような思考の手続きを取っているかを、抽象的に表現した枠組みです。この枠組みには、以下のような活用法があると考えています。
- 過去問演習の復習に活用
110sは、数学の筆記試験における立ち回り方の全体像を提示しているため、過去問演習のたびに、成功要因や失敗要因を特定する事が容易になります。問題選択がうまくいかなかったのか、解法選択に失敗したのか、計算実行に失敗したのか、これらの要因を明確に区別することにより、どの部分を強化する必要があるのかが明瞭になります。これにより、効率的に得点の最適化が可能になると考えます。 - 友人や指導者との議論に活用
模試の帰り道に、友人や指導者と一緒に感想戦をする際に、110sが脳内にあると、感想戦を秩序立てて行うことが可能になります。試験本番における立ち回りの全ての観点を網羅している枠組みなので、成功要因や失敗要因を漏れなく論じることが可能になります。また、各部分について、自分の戦略と友人・指導者の戦略を比較するのも面白いでしょう。 - 普段の学習に活用
110sは試験本番で点を取るための本質的な要素をまとめたものでもあります。問題選択をするための選球眼や、適切な解法選択を行う能力、高速な計算テクニック、検算法は、一朝一夕に身につくものではありません。110sの枠組みが脳内にあることにより、いま自分が学んでいる数学の問題を解く技術が、110sのどの部分に位置づけられるかが明らかになります。これにより、学んだ技術を体系的な枠組みの一部として位置づけることが可能になり、記憶に定着しやすくなります。
では、110s -Double One Zeros – を頭に入れながら、100年後に再び10sを迎えるその時にも通用する、普遍的かつ不変的な、数学筆記試験を攻略する能力を共に身に着けて行きましょう!各論の具体的な内容については、個別に詳述していく予定ですので、今後もメタスキリングをよろしくお願いいたします。




コメント