本記事の目的
本記事では、 東大模試理系数学119/120 、 京大模試総合全国1位 を獲得し、 東大理三に現役合格 したメタスキリング教務主任H.M.(渋谷教育学園幕張高校卒・東京大学医学部医学科)が、東大理系数学2024の講評を執筆します。
この記事では、ただ問題を解く方法を紹介するだけでなく、どの問題に取り組むべきか、どの順番で進めるべきかという、 試験で勝つための戦略 にも焦点を当てます。さらに、一つの問題に対して複数の解法がある場合に、 解法選択をどのように行うか についても掘り下げます。そして、解法を決めた後は、その解法を実行する際の 論理展開 や、間違いを見つけ出す 検算方法 についても、 メタスキリングのオリジナル理論: 数学筆記試験で点を取るためのフレームワーク- 110s に基づいて、詳しく解説していきます。
この記事を読むことで、東大理三生がどのような考え方で、数学の試験に挑んでいるかを感じ取り、試験での成功へと繋がる戦略的アプローチを掴んでいただけましたら嬉しいです。
東大理系数学2024の全体概観
今年の東大数学は2022、2023よりは相対的に易化し、2021並だと思われます。それでも質・量、共に難しいでしょう。理一、理二は1,2,4の 3完 、理三は1,2,4と3or5の 4完 くらいが取れると、数学でアドバンテージが取れるでしょう。ボーダーは理一・理二は55-60点前後、理三は80点前後と思われます。
各問の概要と難易度評価・目標解答時間
難易度は、ABCDの四段階評価。大学への数学の難易度表記に準拠しています。
| 問 | 内容 | 難易度 | 目標時間 |
|---|---|---|---|
| 1 | 円錐と存在範囲 | B | 20分 |
| 2 | 絶対値付きの積分 | B | 20分 |
| 3 | 偶奇に着目する確率漸化式 | C | 40分 |
| 4 | 円と放物線の共有点 定数分離による方程式の解のカウント | B | 30分 |
| 5 | 三角形の回転体 | C | 30分 |
| 6 | 三次多項式が素数となる条件 | D | 60分 |
理一、理二志望者が取りたい問題: 1 2 3(1) 4 6(1)
理三志望者が取りたい問題: 1 2 3(1)(2) 4 5 6(1)
問題選択・優先順位付け
最初に、 メタスキリングのオリジナル理論: 数学筆記試験で点を取るためのフレームワーク- 110s の概観を以下に示します。この理論は、数学の筆記試験で点を取るために必要な各要素を、普遍的な枠組みとして抽出したものです。この理論に基づいて、東大理系数学2024の試験戦略について論じます。
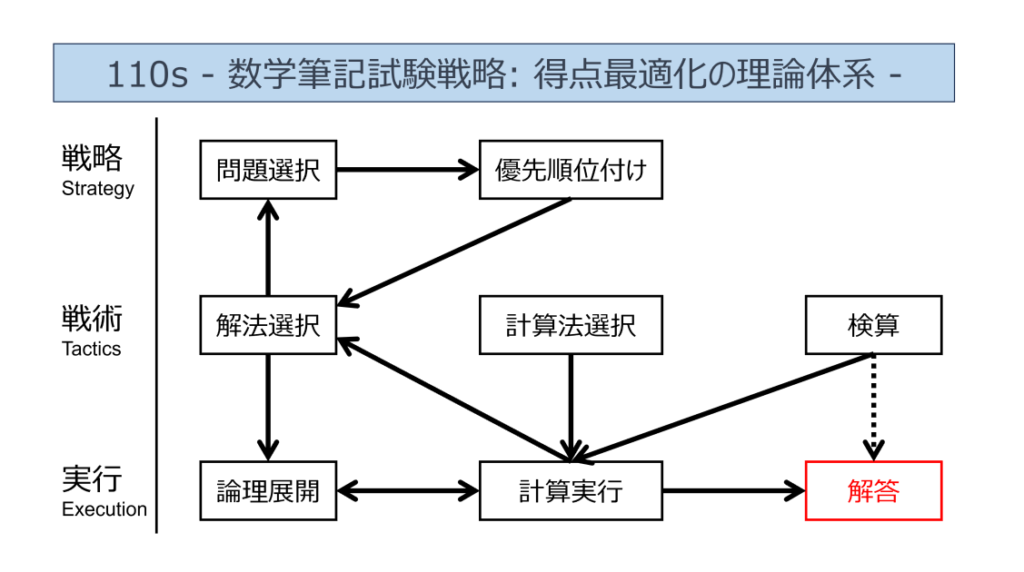
まず最初に、問題の選択と、優先順位付けについて論じます。入試の数学では、 問題の選択と優先順位付け が非常に重要です。要するに、 簡単で計算が軽い問題から順に取り組む ことが大切です。最初に 全体をざっと見て 、5分から10分ほどで どの問題をどの順番で解く か考えましょう。ここでは、私が問題を選択する際に考えたポイントを示します。
第1問: 東大数学頻出の円錐面の方程式の導出をする時の、ベクトルの解法を使えそうで、発想は簡単。計算も比較的軽そう。
第2問: 入試数学でよく出る絶対値付きの積分。場合分けが単純で、arctanやlogが出てきても計算はそれほど重くなさそう。
第3問: 問題文の条件が複雑だが、(1)は調べるだけで済む。(2)と(3)は状況整理が難しそうで、計算量は未知数。
第4問: f(x)の中身がやや複雑。(1)は2点の距離=半径の式と微分係数一致の式を解くだけ。(2)は発想は簡単だが計算は重そう。
第5問: ドーナツ型の問題。グラフの回転体は積分するだけだが、立体図形の回転体は場合分けがある場合が多く図形考察も必要なので、やりにくそう。
第6問: (1)は因数分解で簡単。(2)は抽象的な整式で条件を言い換えるのが難しそう。
この考察に基づいて、 発想が簡単で計算量が軽そうな問題 から順に解くことにしました。具体的には、1→2→4→5→3(1)→6(1)→3→6の順で解きました。
この問題選択で重要なのは、 どんな大問でも(1)は比較的簡単な場合が多い ことです。実際、 第3問の(1)は8点調べるだけ、第6問の(1)は教科書レベルの問題 です。入試数学では、 取れる問題をしっかり取り切る ことが大原則です。
第1問
解法選択
角度の処理
- ①傾きをtanとみて加法定理
- ②ベクトルの内積の利用
が思いつくでしょう。
しかし、①は平面内でしか使えません。また、東大2013-6のような、円錐面の方程式をベクトルを用いて導出する問題の経験があれば、②が選べるでしょう。
論理展開
√A≦Bの同値変形 が途中で出てきます。 √A≦B ⇔ A≦B^2 かつ A≧0 かつ B≧0 の同値変形は証明も含めて覚えておきましょう。 この問題では、√の中身は常に正となりますが、 Bの部分は正だとは限りません。 それを考慮せずに変形すると、答えに x軸より下の部分が含まれてしまいます。
他に頻出な同値変形としては、
- √A≧B ⇔ 「A≧0 かつ B≦0」 or 「A≧B^2 かつ B≧0」
- B/A>0 ⇔ AB>0
- B/A≧0 ⇔ AB≧0 かつ A≠0
があります。証明してみよう。
検算
検算の定石: 領域図示の問題では周上の点が題意を満たしているかCheck
y=|x|と楕円3x^2+(y-1)^2=3の交点は、格子点(1,1),(1,-1)。この2点では、(ii),(iii)のどちらでも等号が成立するはず。整数値で楽なので代入して確かめよう。
H.M.の解いた感想: 解答時間は13分。東大の大好物円錐がまた出たか。難易度は2023の1とは大違いだ…。しかし、易問とはいえ、同値変形をできていない受験生も多そう。
第2問
解法選択
(1) 絶対値付きの積分: 絶対値の中身が0となる点を境界にして場合分け。これはどの問題集にも載っている超典型定石です。
積分の含まれる関数の最大最小
- ① 微分積分学の基本定理 「積分の逆は微分」
- ② 具体的に求めた後、微分
のいずれかが考えられます。ここで(3)に目をやると、f(x)を具体的に求める必要があるのがわかります。よって②を選択するのが良いでしょう。 このとき、tanの逆関数であるarctanが出てくるが、東大なら書いても許されるでしょう。心配なら①。
計算法選択
(2) tan22.5°の導出
- ① 2倍角 を用いて有名角tan45°に結び付ける (数式)
- ②直角二等辺三角形の45°の角に二等分線を引く (図形)
の2つがあるが、①の方が早いだろう。ただ、どちらでも出来るようにしておこう。
今回の場合はtan22.5°を求める必要があったが、他の角度ではどのような計算法が考えられるかについても、検討してみよう。
tan36°の導出 ①θ=36°として、 tan3θ=-tan2θ に、 3倍角 と 2倍角 を用いる (数式) ② 36°,72°,72° の二等辺三角形の72°の角に二等分線を引き、新しくできた三角形に 相似 を適用する (図形) の2つがあるだろう。参考書は②の解法を採用しているのが多いですが、①でも出来るようにしておこう。(36°の三角比は東大1994-2でも出題済)
H.M.の解いた感想: 解答時間は15分。最近の東大らしくない典型問題。
第3問
解法選択
確率漸化式の論点
- ① 偶奇 に着目(慶医2001-2、東大2004-6、東大2012-2、名大2017-2、東工大2018-5など)
- ② 対称性 に着目し文字の種類を減らす(名大2018-4など)
- ③隠れた条件、 確率の総和は1 に注意(九大2018-3など)
は難関大特有の論点です。
①についてですが、 自然数nに対しての問題 は、 n=1,2,3という 小さい数字で実験 これで、偶数の時は、(2,1),(-2,-1),(-1,2),(1,-2)のいずれかにいて、奇数の時は、(2,-1),(-2,1),(-1,-2),(1,2)のいずれかにいることがわかります。
②についてですが、本問の(2)が誘導になっています。
以上の①、②より、8点間の移動についての問題が、2文字の確率漸化式へと帰着できます。
2文字が絡んだ確率漸化式は、漸化式を2本立てる必要がありますが、一方は③に着目すれば立式できます。
検算
検算の定石: 確率漸化式
- ①確率は 0以上1以下
- ② n=1,2,3 で成立するかCheck
- ③ 定常状態(n→∞) で成立するかCheck
①は自明でしょう。 ②ですが、逆に n=1,2のみ別個に場合分けが必要な時 もあるので、扱いには注意が必要。 ③ですが、本問では、nが偶数とすると、n→∞のとき、 4点(2,1),(-2,-1),(-1,2),(1,-2)にいる確率は均等になりそう だと、予想が立てられます。よって、n→∞でpn→1/4と予想できますが、実際これは 答えの極限と一致 しています。このように定常状態を考えることで検算できます。(これは東大2012-2でも使える検算術)
H.M.の解いた感想: 解答時間は34分。(3)で4文字の漸化式を立てて面を食らうが、落ち着いて定石に立ち返ればなんてことはないですね。
第4問
解法選択
(1) c(t)とr(t)と、未知数が2つなので、 2本の式 を立てる必要がある。 2点間距離が半径に等しい ということから 距離の情報 から1本立てれる。 もう1本は、 接点における傾きの情報 から立てれる。この立式は 接線 に着目する方法と、 法線 に着目する方法の2パターンがあります。
f(x)の 接線 に着目
- ①円を陰関数表示して、dy/dxを求め、これが接線の傾きf’(t)と一致
- ②円の中心と接点を結ぶ直線の傾きと、接線の傾きf’(t)の積が-1
- ③円の中心から接点を結ぶベクトルと、接線の方向ベクトルが垂直 (⇔内積0)
の3通りの方法が考えられます。しかし、①は接点のy座標が中心のy座標と一致するとき、②は接点のx座標が中心のx座標と一致するとき、 0除算が発生し、傾きが未定義になる ので、それが起こらないことを議論する必要があります。よって、本問では、接線に着目するとき ③で立てると良いです。 また、本問とは関係ないが、②、③は 円のみで成り立つ解法 であることに注意が必要である。例えば楕円の場合は ①しか使えません。
f(x)の 法線 に着目
④f(x)のx=tにおける法線が円の中心を通る
この解法は、 f’(t)が0になるとき、0除算が発生 するので議論が必要です。しかし本問では0にならないのは自明なので、これでも良いだろう。
以上から、 ③あるいは④の解法を選択すると良いです 。
(2) 三次以上の方程式の実数解の個数 を求めるには、以下の方法が考えられる: ① (極大値)×(極小値) と0の大小関係 (3次方程式) ②a=g(t)の形に 定数分離 今回は、4次の場合なので②を用いよう。
検算
検算の定石: 極端な場合で検算せよ
今回のケースは、0<t<4であるので、極端な場合とは、その変域の端点、t=0とt=4の場合です。これらを 代入した結果が、図形的考察と一致するか を確かめる。
- t=0のとき、中心は原点で、半径は4√2であること
- t=4のとき、円は潰れて点(4,0)であること
はそれぞれ図形的に考えれば明らかであり、r(0)=4√2、c(0)=0、r(4)=0、c(4)=4から、数値を代入した結果とも一致することを確認できます。
H.M.の解いた感想: 解答時間は24分。複二次式出てくると思いきや、期待を裏切られ面を食らう。係数も汚いし計算ミスが恐ろしい…3次式の2乗は計算ミス起こりがちなのでひやひやしますね。
第5問
解法選択
立体図形の回転体: 回転軸に垂直に切って、回転軸からの最長距離Max、最短距離minを求めて、π(Max^2-min^2)を回転軸に沿って積分(ドーナツ型)。これは超典型定石。
ここで、最長距離、最短距離を求める際には、 ① 図形的 に解く ② 数式的 に解く の2つの方向性があります。 このとき、 ②は①に劣る解法 と言えます。なぜなら、図形的にわかることをわざわざ数式を持ち出して説明しているからです。
①、②について具体的に話していきます。
①図形的に解く まず、題意の図形を図示してみる。すると、 xが1/2を境に図形が変化 していることがわかります。 次に、平面x=kと三角形の交線を求めると、線分であることが分かります。 あとは、この線分の点の、平面x=k上の原点からの最長距離Max、最短距離minを求めればよいです。 Maxは明らかでしょう。 Minを求めるとき、注意することとしては、 線分が垂線の足を含むかどうか の議論である。含む場合は、 垂線が最短 となる。それは k=1/3 のときです。 この場合分けに気づけるかが本問最大の鍵です。
②数式的に解く 三角形の周と内部は、ベクトルを用いて表示できる のであった。三角形の周と内部にある任意の点Pは、OP→ = OA→ + s AB→ + t AD→ (s≧0,t≧0,s+t≦1) とかけます。 これを用いて式変形を行うと、断面の式が数式的に求まります。 この方法で解いても、 線分が垂線の足を含むかどうか の議論は必要になってくるので、注意が必要です。
このように、②は場合分けも特に省略できるわけでもない、図でわかる断面の式を大げさに求める解法と言えます。
検算
検算の定石: 極端な場合で検算せよ 第5問でも、第4問と同様に、極端な場合-端点での検算術-が有用です。 本問の場合、 最大の落とし穴であるk=1/3の議論を忘れても、端点の場合を検算することにより、そのミスに気付くことが出来ます。 たとえば常に、線分が原点からの垂線の足を含むと勘違いして、min=(1-k)/√2だと思ってしまった場合を考えよう。 このとき、x=kの変域は、0≦k≦1であるので、端点であるk=0のときを考えてみると、断面の図形は1点(0,1,0)となる。よって、原点からの距離のMaxもminも1になるはずです。しかし、min=(1-k)/√2に代入すると、min=1/√2なので 矛盾が起きます 。これにより、線分が原点からの垂線の足を含む場合と、そうでない場合に、場合分けが必要であると、気付くことが出来ます。 このように、 端点での検算により、場合分け忘れなどの致命的な議論の誤りも正せる ことがあります。
H.M.の解いた感想: 解答時間は28分。最初k=1/3の場合分けに気付かず首をかしげたが、検算で気付けた。最後の最後の数2の積分でミスはしないように。
第6問
解法選択
整数問題の3大定石
- ① 積の形 に変形
- ② 範囲 を絞る
- ③ 余り に着目
(1) ①を用いれば、容易。
(2) g(n)が素数であるとき、 (i) 「n=1,a+b+1が素数」 (ii)「n=-1,a-b-1が素数」 (iii) 「n=p(pは素数),p^2+ap+b=1」 (iv) 「n=-q(qは素数),q^2-aq+b=-1」 のいずれかの条件が成り立つ。
ここで、(i)から生じうるnの個数は1個、(ii)は1個、(iii)は2個、(iv)は2個です。 また、いずれも個々で考えれば、どれも成立しそうです。 よって、 ある特定の条件下では、他の条件が成立しない 、ということを示せばよいとわかります。
(i),(ii)は緩い条件なので、大半の場合で成立しそうです。 しかし、(iii),(iv)は二次式の解であり、成立の可能性は低そうです。 よって、特定の条件下で、(iii),(iv)の条件が成立しない、というのを示す方針を取ることとなります。
(I) (iii),(iv)が同時に成立すると仮定する。 ①積の形に変形 を意識すると、二次式同士の差を取る方針が思いつきます。すると矛盾が出てきます。
(I)から、(iii),(iv)が同時に成立しないことが示されるため、4個以下であることは確定です。あとは4個中1個削るのを考えればよいです。 (II),(III)は、(iii),(iv)を(i),(ii)のa,bの条件と結びつけるために、解と係数の関係を使うのがベストです。 また、(i),(ii)の素数である、という条件は扱いにくいので、素数⇒正であると言い換えた方が見通しが良いです。
(II) (i),(ii)の条件の下で、(iii)が2個の素数解(p1,p2)をもつとする。 (i),(ii)から、(a+b+1)+(a-b-1)=2aは素数の和なので、aは正である。 しかし、解と係数の関係から、p1+p2=-a<0となり矛盾。 よって(i),(ii)の条件下では高々1個しか(iii)は素数解をもたない。
(III) (i),(ii)の条件で、(iv)が2個の素数解(q1,q2)をもつとする。 q1+q2=a (これ単体では絞れない) q1q2=b+1 ここで、 (i),(ii)の条件に代入してみると、 q1+q2+q1q2が素数(⇒正である) q1+q2-q1q2が素数(⇒正である) 第1式は常に成り立つので意味がない。 第2式から、q1+q2>q1q2となる。 この不等式をよく見ると、 左は1次式、右は2次式 となっています。よって、 q1,q2が十分大きいとき、この不等式は成り立たない ということがわかります。あとは、q1,q2が2以上であることから、この不等式が成立しないことを言って矛盾を示そう。 q1+q2>q1q2 ⇔ (q1-1)(q2-1)<1 (① 積の形 に変形) q1-1≧1、q2-1≧1なので、この不等式は成立せず矛盾。 よって(i),(ii)の条件下では高々1個しか(iv)は素数解をもたない。
以上の(I),(II),(III)から、高々3個しかf(n)が整数となるnは存在しないとわかります。
論理展開
解の個数が4個以上となるパターンは以下の8パターンです。この8パターンを 漏れなく 否定することが本問では重要です。
| パターン | (i) | (ii) | (iii) | (iv) | 解の個数 | 否定する根拠 |
|---|---|---|---|---|---|---|
| パターン1 | 1 | 1 | 2 | 2 | 6 | (I)でこの可能性は否定 |
| パターン2 | 1 | 0 | 2 | 2 | 5 | (I)でこの可能性は否定 |
| パターン3 | 0 | 1 | 2 | 2 | 5 | (I)でこの可能性は否定 |
| パターン4 | 1 | 1 | 1 | 2 | 5 | (I)でこの可能性は否定 |
| パターン5 | 1 | 1 | 2 | 1 | 5 | (I)でこの可能性は否定 |
| パターン6 | 1 | 1 | 1 | 1 | 4 | (I)でこの可能性は否定 |
| パターン7 | 1 | 1 | 2 | 0 | 4 | (II)でこの可能性は否定 |
| パターン8 | 1 | 1 | 0 | 2 | 4 | (III)でこの可能性は否定 |
大問6(2)の全パターン
H.M.の解いた感想: 150分内では終わらず…。(2)で4個以上のパターンが多く混乱。落ち着いて条件を見つめてようやく(I)に気付く。それでも素数は正であるということを用いるのに時間がかかり、(II)(III)に苦戦しました…。
終わりに
以上、東大理系数学2024の講評・戦略となります。 このように、東大理系数学のような、高難易度の数学試験で高い得点を取るには、問題選択や、解法選択、論理展開、検算方法などを駆使しながら、戦略的に問題を解き進めていく必要があります。
メタスキリングでは、このように、高難易度数学の試験で要求される能力を、抽象的にまとめ上げた オリジナル理論: 数学筆記試験で点を取るためのフレームワーク- 110s に基づいて、今後も大学受験に関する記事を執筆していきます。また、メタスキリングでは、現在オンラインでの指導を承っております。詳細は、お問い合わせページをご参照ください。