東大理系数学は、第1問が簡単で、第6問が難しいか？大数・赤本・青本・鉄緑会の難易度評価とその分析

はじめに

東京大学理系数学の問題には、第1問が比較的簡単で、第6問に至っては非常に難しいという風潮が存在しますが、これは真実なのでしょうか？本記事では、まず、メタな視点から、各問題の難易度について、仮説を立てた後、次にデータに基づいて、この仮説を検証します。具体的には、過去30年分の東大理系数学の問題について、大手予備校・出版社の難易度評価（大数、赤本、青本、鉄緑会）を集計し、仮説が本当に正しいのかどうか、難易度評価のデータを用いて検証します。

対象読者

東京大学理系学部を志望する受験生
東大理系数学の難易度評価に興味がある受験生や教育関係者

注意事項

本記事で使用するデータは、市販されている参考書の難易度評価に基づいています。
- 難易度評価を付ける側は、どの問題が第1問で、どの問題が第6問かを既に知ってしまっているため、問題番号による先入観が入った評価になっている可能性があります。(盲検ではない)
この難易度評価の集計結果は、「第1問は簡単」で「第6問は難しい」という傾向を保証するものであり、実際の本番の試験での難易度は、傾向とは異なる可能性があり得ます。
本番の試験では、先入観を入れずにフラットな視線で問題を眺めましょう。そのうえで、残り時間が少ないが、まだ解けていない問題が沢山あるときに、どの問題を解くか、選択をするひとつの基準として、この集計結果を思い出すと役に立つかもしれません。

メタな視点からの各問題の難易度の考察

まずは、東大理系数学の各問題の難易度を、メタな視点から分析します。ここでいう「メタな視点」とは、入試問題そのものの内容ではなく、作問者の意図、問題の配置、解答用紙のサイズなど、問題の外側に関する情報を基に、問題に対する洞察を得るアプローチのことを指します。

メタ情報1: 問題の配置と難易度

まず最初に、大学教授がどのような手順で入試問題を作成するかについて考えてみましょう。推測では、教授たちはまず、各分野（代数、幾何、解析）から出題する問題数を決めます。その後、個々の問題について難易度と計算量を評価し、それぞれの問題をどの順番で配置するかを決定すると考えられます。

この問題配置のプロセスにおいては、次のような仮説を立てることが出来ます。：

第1問は、試験の初めに緊張している受験生を安心させる目的で、比較的解きやすい問題を選ぶ。
第6問は、試験時間が進み、多くの受験生が時間に追われている状況を考慮して、挑戦しづらい難問を配置することで、受験生の能力を最大限に引き出す。

このように、問題の選定と配置は、受験生の心理状態や試験の進行を考慮しながら、総合的に決定されていると推測されます。

メタ情報2: 解答用紙の大きさと計算量

次に、別のメタ情報である解答用紙の大きさから、問題について言えることを考えましょう。東大理系数学では、各大問ごとに、与えられている解答スペースの大きさが異なります。

第1問、第2問、第4問、第5問は、A3の半分の大きさの解答スペースが与えられています。
第3問、第6問は、A3を全て使う解答スペースが与えられています。

このメタ情報から、「第3問・第6問には、大きな解答スペースを使う必要がある、計算が重たい問題を配置しているのではないか。」という仮説を立てることが出来ます。

こうしたメタ情報から得られる仮説は、あくまで推測でしかありません。ここからは、過去30年分に出題された東大理系数学の問題について、予備校が下した難易度の評価を検証して、以下の二つの仮説を検証していきます。

仮説1: 東大理系数学は、第1問が最も簡単で、第6問が最も難しい。
仮説2: 東大理系数学は、第1,2,4,5問の計算量が軽く、第3問・第6問の計算量が重い。

本記事では、仮説1を検証します。

各予備校の難易度の集計

ここでは、大数・赤本・青本・鉄緑会が提供する過去数年間の東大理系数学の問題ごとの難易度評価を集計し、分析します。それぞれの予備校が独自の基準で難易度を評価していることから、複数の視点から仮説の検証を行うことが出来ます。

赤本

まずはみなさんおなじみの教学社の「赤本」からです。

集計期間

1997年度から2021年度の東大理系数学

難易度評価

A,B,C,Dの四段階評価

集計結果

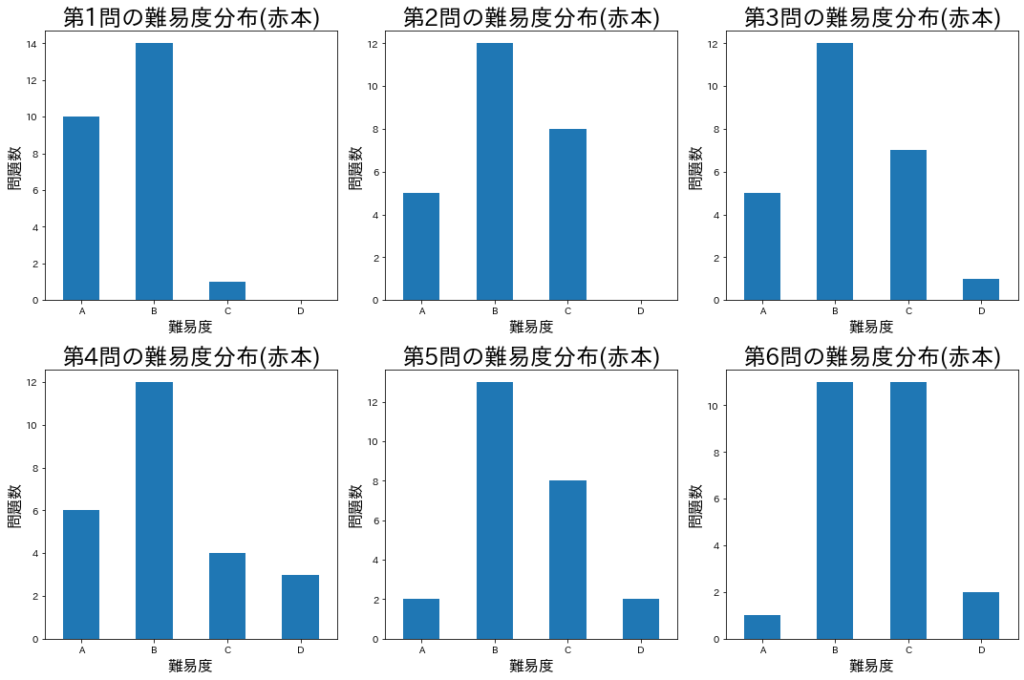
第1問は25問中24問がA,B問題であり、C問題に至っては2009年度の1問しかありません。
一方、第6問は、A問題は1問のみであり、B問題C問題が大半を占めます。
やはり第1問は解きやすい問題が多く、第6問は解きにくい問題が多いようです。ただ、第6問であっても、標準的な難易度であるB問題は25問中11問出題されており、「捨て問」だとして切り捨ててしまうのは危険でしょう。

大学への数学

次に、大学への数学が毎年出している、難易度評価の集計を行います。

集計期間

1993年度から2023年度の東大理系数学

難易度評価

A,B,C,Dの四段階評価

集計結果

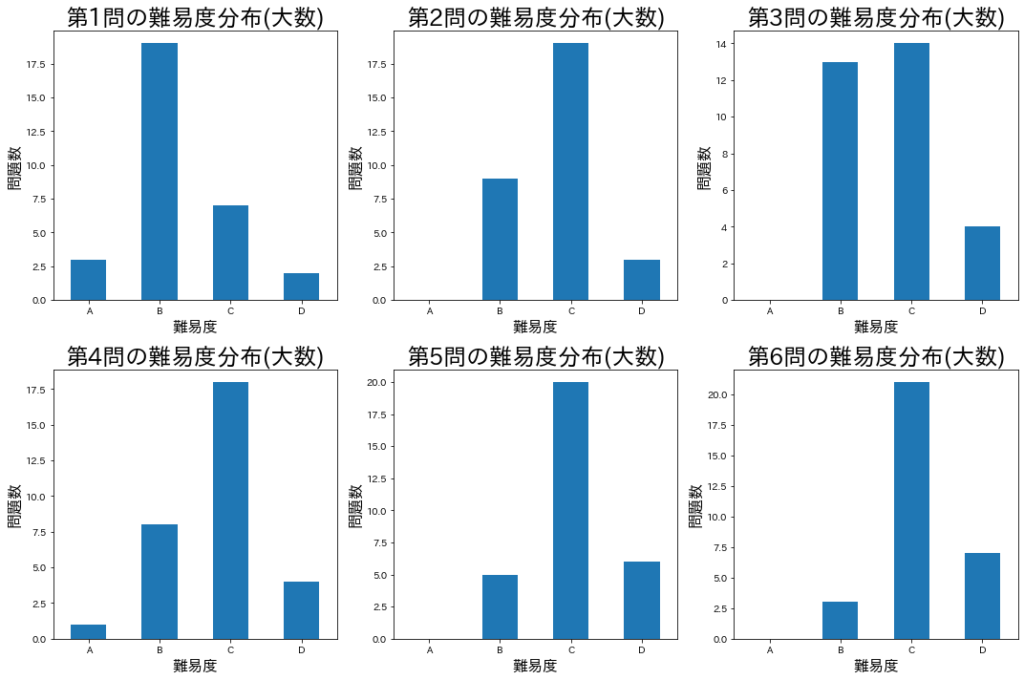
第1問は31問中21問がA,B問題、第6問は31問中28問がC,D問題となりました。赤本での評価と比較すると、大学への数学の難易度評価では、顕著に「第1問が解きやすく、第6問が解きにくい」という傾向が表れています。

青本

次に、駿台が毎年出版している「青本」から難易度評価です。

集計期間

1999年度から2023年度の東大理系数学

難易度評価

A,B,C,D,Eの五段階評価

集計結果

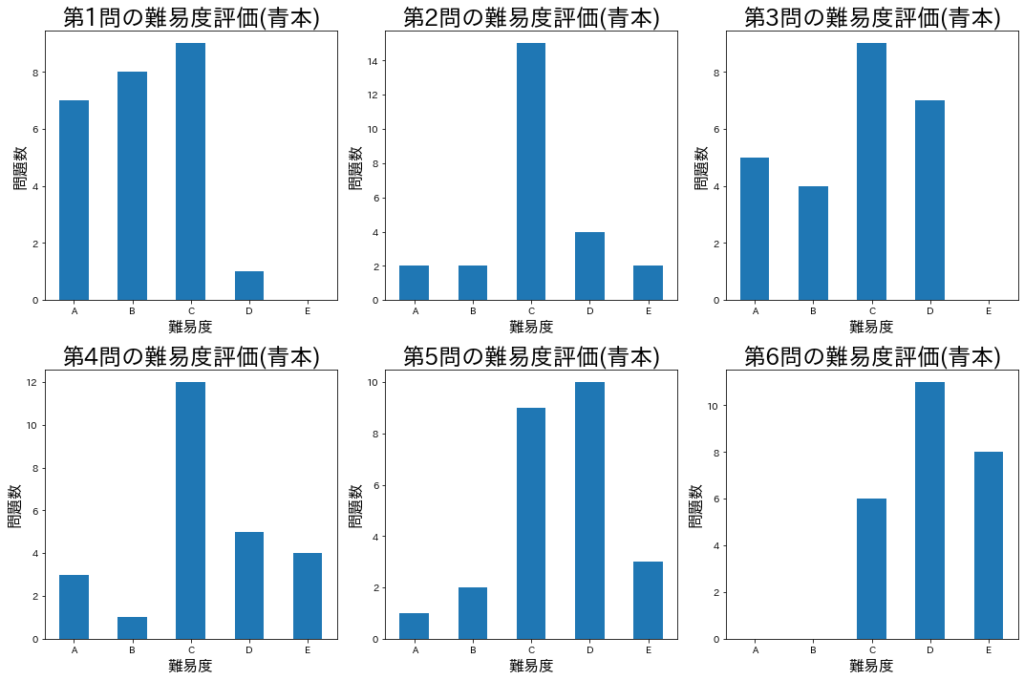
第1問は25問中24問がA,B,C評価(標準難易度以下)、第6問は、25問中25問がC,D,E評価(標準難易度以上)となっています。ただし、第6問であっても、25問中6問はC評価(標準難易度)となっているため、捨て問と切り捨てるのはやはり危険です。

鉄緑会

最後に、鉄緑会から出版されている「鉄緑会東大数学問題集」から難易度評価です。

集計期間

1980年度から2019年度の東大理系数学

難易度評価

発想、計算、時間、論理の4つの項目について、A,B,Cの三段階評価
本記事では、「発想」の評価を難易度の評価に使用

集計結果

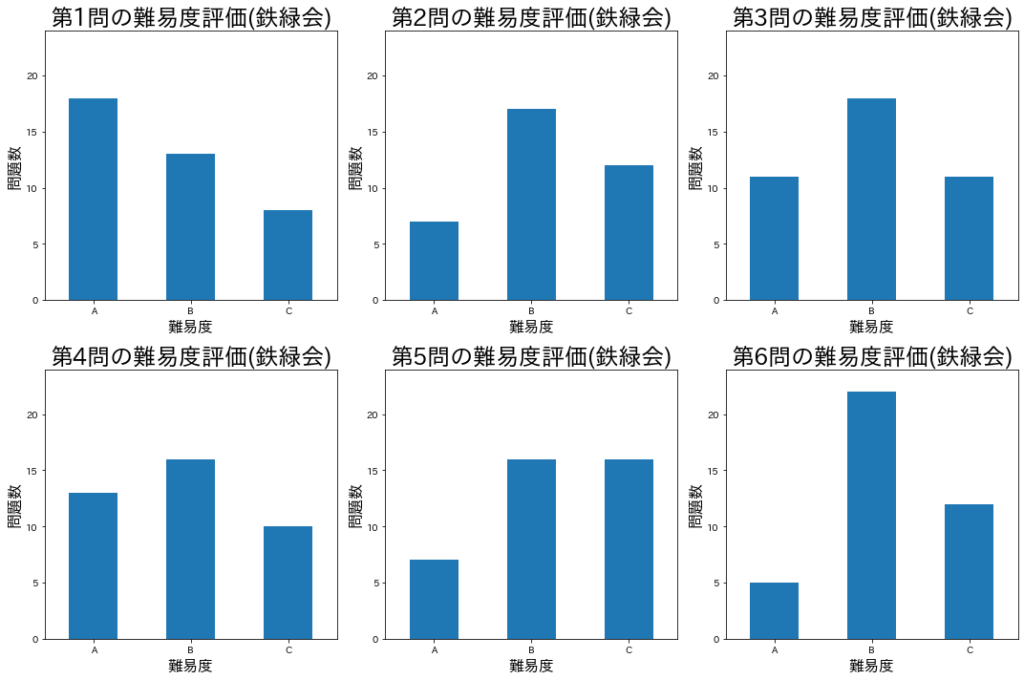
第1問は40問中31問がA,B評価、第6問は40問中35問がB,C評価となっています。
集計期間が1980年度と昔の年度のものも集計しているため、今と傾向が異なっている可能性があります。

各問題の難易度評価の指標

以上、四予備校が出している難易度評価に基づいて、東大理系数学の第1問と第6問に難易度の差があるのか、仮説を検証しました。概ねありそうだという傾向は見受けられたものの、棒グラフ同士の定性的な比較では、それぞれの難易度の違いを定量的に評価する事が難しいため、以下のような評価の指標を導入します。

難易度評価指標 – 期待得点の定義

この指標は、20点満点の大問のうち、何点を期待値として取ることが出来るか、という意味を持っている指標です。式の詳細は、以下に記しますが、興味のある人だけご覧ください。

難易度評価の集計結果を(A,B,C,D)=(a,b,c,d)と表す
- 例えば、(A,B,C,D)=(10,10,5,5)は、30年分の出題について、A難易度が10問、B難易度が10問、C難易度が5問、D難易度が5問出題されたことを表します。
各難易度の平均得点率を定義
- 東大理系合格者の平均では、得点率が、部分点も含めてA問題90%、B問題60%、C問題25%、D問題5%であると仮定します。
難易度の集計結果と、各難易度の平均得点率に基づいて、期待得点を計算
- 計算式は、(a*0.9+b*0.6+c*0.25+d*0.05)/(a+b+c+d)*20です。
- 例えば、(A,B,C,D)=(10,10,5,5)の場合は、期待得点は11点と計算出来ます。

これらの指標を用いて、各問題の難易度を総合的に評価します。

第1問から第6問の期待得点

上記で定義した、期待得点指標に基づいて、各問題の期待得点を計算した結果が以下の表です。

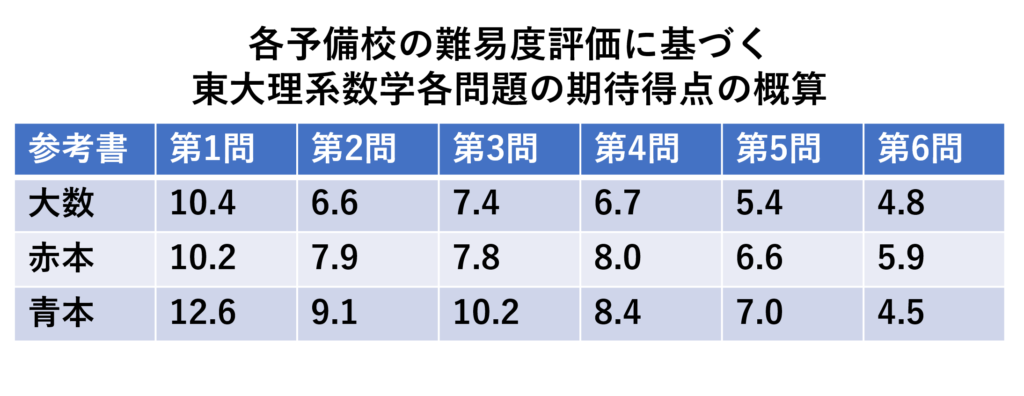
やはり、第1問が最も取り組みやすく、第6問が最も取り組みにくいようです。また、第2問から第4問の期待得点には差が見られませんが、第5問はどの予備校でもやや低めの値となっており、第5問についても、やや取り組みにくい傾向にあることが読み取れます。

(計算方法の詳細)

赤本と大学への数学、青本のそれぞれで難易度評価の基準が違うため、独断で以下のような平均得点率を定義しています。
- 大数: (A,B,C,D)=(0.95, 0.6, 0.25, 0.05)
- 赤本: (A,B,C,D)=(0.7, 0.4, 0.25, 0.05)
- 青本: (A,B,C,D,E)=(0.9, 0.6, 0.5, 0.2, 0.05)
鉄緑会の難易度評価は三段階評価と粒度が低いため、除外しました。

結論

本記事では、東大理系数学の各問題の難易度について、四予備校の難易度評価データと、独自に定義した難易度評価指標を基に、実際に第1問が最も簡単で、第6問が最も難しいという仮説を実証しました。分析の結果、この傾向は一定程度存在するものの、年によっては例外も見られることが明らかになりました。冒頭にも述べた通り、例外は常に存在するため、本記事の内容は、あくまでも時間が無いけれど、問題選択をしなければならない状況に追い込まれたときに、思い出して使うというような活用をされると良いと思います。

この記事を通じて、東大理系数学の攻略に向けた新たな視点を提供できれば幸いです。